Archivo de la etiqueta: grado profesional

El transporte musical

Publicado el por
El transporte musical consiste en escribir o interpretar una pieza musical en una tonalidad diferente a la original. Cambia la altura de las notas, pero no la relación interválica entre ellas. Por eso, la pieza sigue siendo reconocible a pesar de sonar más aguda o más grave.
Recomiendo la lectura del siguiente artículo sobre "lectura y escritura musical para instrumentos transpositores", escrito por José Rodríguez Alvira y publicado en su web www.teoria.com
Ya que existen multitud de instrumentos transpositores, la técnica del transporte no sólo resulta muy necesaria para estos instrumentistas sino también para los compositores y para los directores de orquestas y bandas. 
El transporte puede ser escrito o mental. Por ejemplo: un instrumento transpositor como el clarinete en si bemol, reproduce todas las notas una 2ª mayor por debajo de lo escrito. Es decir: cuando toca con la digitación necesaria para hacer un do, en realidad suena un si bemol. 

Si un clarinete en si bemol tocase esta melodía escrita en Do Mayor
En realidad sonaría así: en Si bemol Mayor

Esto le crearía un problema al compositor que quiera escribir una obra para clarinete solo o acompañado de otros instrumentos. Si el compositor quiere que suene la melodía en Do Mayor y que no choque con el acompañamiento que otros instrumentos le harán en la tonalidad de Do Mayor, tendrá que compensar el hecho de que ese clarinete va a sonar una 2ª Mayor por debajo de lo escrito, dándole una partitura escrita una 2ª Mayor por encima de lo que quiere que suene. Para que suene en Do Mayor, deberá darle una partitura escrita en Re Mayor.

El compositor deberá dar al clarinetista esta partitura en Re Mayor

Si quiere que suene esta melodía en Do Mayor
Este sería un ejemplo de transporte escrito: el compositor inventa y escribe una melodía en Do Mayor. Si quiere que la toque un violín, no necesita hacer nada más, ya que el violín no es un instrumento transpositor. Sin embargo, si quiere que la toque un clarinete en si bemol, necesita escribir la melodía transportada una 2ª Mayor ascendente.
Veamos un ejemplo de transporte mental: Si esa melodía aparece en una partitura para orquesta o banda, en la que se mezclan varios instrumentos transpositores y no transpositores, el director se encontrará con un montón de pentagramas escritos en diferentes tonalidades. Deberá imaginar cómo suenan en realidad todas esas melodías, así que algunas deberá transportarlas mentalmente. Con un poco de práctica, esto puede hacerse si se imagina otra armadura y otra clave.

Por ejemplo: para averiguar cómo sonaría nuestra última partitura en Re Mayor...
...el director se la imaginará sin armadura y la leerá en clave de Do en cuarta. Así:

Aquí vemos un fragmento de la 9ª sinfonía de Beethoven. Aparece solamente la sección de viento madera. Los clarinetes en Si bemol tienen una armadura diferente al resto de los instrumentos, que no son transpositores. Sin embargo, todos suenan en la misma tonalidad.

El cambio de clave y de tonalidad podría parecer suficiente para hacer el transporte mental, pero hay una dificultad añadida: las alteraciones accidentales. Algunas de estas alteraciones podrían cambiar de signo. Imaginemos por ejemplo que una melodía en Do Mayor tiene algunas notas alteradas con sostenidos. Si transportamos la melodía a una tonalidad con varios sostenidos en la armadura (por ejemplo, a Si Mayor, que tiene 5 sostenidos), resulta evidente que no podré alterar con sostenidos aquellas notas que ya tienen sostenido en la armadura (fa, do, sol, re y la). Si quiero alterar esas notas ascendentemente, tendré que ponerles un doble sostenido y si quiero alterarlas descendentemente no les pondré un bemol, sino un becuadro. En cambio, el "si" y el "mi" no aparecen en la armadura y por eso sí podría alterarlas con un sostenido accidental.
Hay un sistema para calcular qué notas cambiarían el signo de la alteración cuando efectuamos el transporte. Es el sistema de las diferencias. Las diferencias serían aquellas notas que sí cambian el signo de la alteración con respecto a la melodía original (en el ejemplo anterior: las notas fa, do, sol, re y la). Estos son los pasos para calcular las diferencias. Lo entenderéis mejor cuando veáis el ejemplo.

Paso 1. Si la nueva tonalidad tiene más sostenidos o menos bemoles que la tonalidad original, o si pasa de bemoles a sostenidos, hablaremos de diferencias ascendentes.
Si la nueva tonalidad tiene menos sostenidos o más bemoles que la tonalidad original, o pasa de sostenidos a bemoles, hablaremos de diferencias descendentes.

Paso 2. Si las armaduras de la nueva tonalidad y de la tonalidad original son del mismo signo (las dos son de sostenidos o las dos son de bemoles), se resta el número de bemoles o de sostenidos de una y otra tonalidad. Si las armaduras son de distinto signo (una es de bemoles y otra es de sostenidos), las alteraciones de ambas armaduras se suman.
El resultado de la resta o de la suma, según corresponda, nos dará el número de diferencias (ascendentes o descendentes según lo visto en el paso 1).

Paso 3. Si las diferencias son ascendentes, llevan el mismo nombre que las notas de la serie de sostenidos que utilizamos en las armaduras (fa-do-sol-re-la-mi-si)
Si las diferencias son descendentes, llevan el nombre de las notas de la serie de bemoles (si-mi-la-re-sol-do-fa)

Paso 4: Las notas que en la nueva tonalidad coincidan con las diferencias ascendentes, cambiarán las alteraciones accidentales de la siguiente forma:
- el doble bemol pasa a bemol
- el bemol pasa a becuadro
- el becuadro pasa a sostenido
- el sostenido pasa a doble sostenido
Las notas que en la nueva tonalidad coincidan con las diferencias descendentes, cambiarán las alteraciones accidentales de la siguiente forma: 
- el doble sostenido pasa a sostenido
- el sostenido pasa a becuadro
- el becuadro pasa a bemol
- el bemol pasa a doble bemol

Veamos un ejemplo: Si pasamos de Re Mayor, que tiene 2 sostenidos, a Si Mayor, que tiene 5 sostenidos...
- las dos armaduras son del mismo signo (sostenidos), así que se restan. 5 - 2 = 3 diferencias
- como pasamos de menos sostenidos a más sostenidos (de 2 a 5 sostenidos), las diferencias son ascendentes.
- como tenemos 3 diferencias ascendentes, las notas que cambiarán el tipo de alteración accidental con respecto a la melodía original, serán las 3 primeras notas de la serie de sostenidos: "fa", "do" y "sol". El resto de notas no cambiarán el tipo de alteración accidental.
- las notas fa, do y sol de la nueva tonalidad (Si Mayor) no tendrán la misma alteración accidental que en la melodía original, sino que cambiarán de manera ascendente (el doble bemol pasa a bemol, el bemol pasa a becuadro, el becuadro a sostenido y el sostenido a doble sostenido).

Por tanto, para transportar esta melodía en Re Mayor...
...a Si Mayor, cambiamos la armadura y bajamos todas las notas una tercera. Cono tenemos 3 diferencias ascendentes, las notas "fa", "do" y "sol" de la nueva tonalidad no tendrán la misma alteración accidental que la nota correspondiente en Re Mayor. Vemos que el mi sostenido pasa a do doble sostenido y que el si bemol pasa a sol becuadro. El cambio, el resto de las notas no cambia el tipo de alteración accidental.


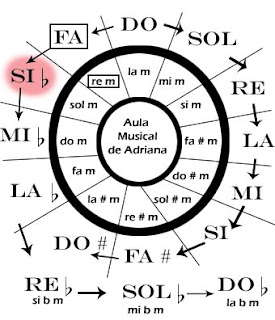
Es fácil calcular el número y tipo de diferencias si nos fijamos en el círculo de quintas.

Cuando avanzamos de una tonalidad a otra siguiendo el sentido de las agujas del reloj, vamos sumando diferencias ascendentes. Por ejemplo, de Sol Mayor a Mi Mayor, tenemos 3 diferencias ascendentes.
Si pasamos en la otra dirección tendremos diferencias descendentes. De Sol Mayor a Si bemol Mayor tendremos 3 diferencias descendentes.
Hay que tener cuidado con el círculo de quintas en el momento en que hacemos la enarmonía: recordemos que aunque cerremos el círculo para hacer el esquema, en realidad es como una espiral, tal como muestro en el siguiente dibujo. En el sentido de las agujas del reloj, después de Fa # Mayor no va Re b Mayor, sino Do # Mayor. En el sentido contrario, después de Re b Mayor, va Sol b Mayor.

¿Qué pasaría si tengo que transportar una melodía escrita en Si bemol Mayor (2 bemoles) una tercera menor ascendente? Pues que la melodía transportada estaría en Re bemol Mayor, con una armadura de 5 bemoles y tendríamos 3 diferencias descendentes. Por eso, cuando en Re bemol mayor escriba las notas "si", "mi" y "la" no me bastará con copiar la misma alteración que tuvieran las notas correspondientes en Si bemol Mayor, sino que cambiarán en sentido descendente (los sostenidos pasan a becuadros, los becuadros a bemoles, etc.).
Este es un tema complicado, que vemos en 2º de grado profesional. A medida que vayáis haciendo ejercicios, lo comprenderéis mejor.
Mientras preparo ejercicios nuevos sobre el transporte, os recomiendo que hagáis estos de la página www.teoria.com

Ejercicio de lectura de melodías para instrumentos transpositores

Ejercicio de escritura de melodías para instrumentos transpositores

Ejercicio de equivalencias

Publicado el por
Tal como os prometí en la última entrada del blog, aquí tenéis un ejercicio para comprobar que entendéis perfectamente el tema de las equivalencias musicales en los cambios de compás.
Pinchad el enlace para acceder. El ejercicio consta de cuatro preguntas. Debéis pinchar en las imágenes para que se hagan más grandes. Después se cierran en la cruz y se contesta a la pregunta. Cuando terminéis las cuatro, pincháis en "finalizar" y podréis ver la corrección. ¡Suerte!

Pinchad aquí si queréis volver a leer la explicación de las equivalencias.

Ejercicio de equivalencias

Publicado el por
Tal como os prometí en la última entrada del blog, aquí tenéis un ejercicio para comprobar que entendéis perfectamente el tema de las equivalencias musicales en los cambios de compás.
Pinchad el enlace para acceder. El ejercicio consta de cuatro preguntas. Debéis pinchar en las imágenes para que se hagan más grandes. Después se cierran en la cruz y se contesta a la pregunta. Cuando terminéis las cuatro, pincháis en "finalizar" y podréis ver la corrección. ¡Suerte!

Pinchad aquí si queréis volver a leer la explicación de las equivalencias.

Cambios de compás: las equivalencias

Publicado el por
Es frecuente encontrar obras en las que se producen cambios de compás. En determinado momento de la partitura, podemos encontrar una doble barra y una indicación de compás diferente a la inicial. No por ello se detiene la pieza, sino que la música debe pasar fluidamente de un compás a otro.
Puede haber varias posibilidades:
1. Que la velocidad del pulso se mantenga (lo que se indica con las llamadas equivalencias de pulso igual a pulso)
2. Que la velocidad del pulso cambie, pero la duración de las figuras se mantenga (lo que se indica con las llamadas equivalencias de figura igual a figura)
3. Que la velocidad del pulso y de las figuras cambie (lo que se indica con nuevas expresiones de tempo)

¿Cómo sabemos si la velocidad del pulso debe cambiar o no? Gracias a las equivalencias. Las equivalencias son relaciones entre dos figuras, cada una perteneciente a un compás distinto, que van a tener la misma duración y por eso van unidas por el símbolo =.

Caso 1: Si queremos que la velocidad del pulso se mantenga, escogemos las figuras que ocupan un pulso en cada compás y las igualamos. Para pasar de 2/4 a 3/4, escribiría "negra = negra" y para pasar de 2/4 a 6/8 escribiría "negra = negra con puntillo", ya que la figura que ocupa un pulso en 6/8 es la negra con puntillo.
La equivalencia se escribiría sobre la doble barra. Por lo general, la primera figura equivale al pulso del primer compás y la segunda figura equivale al pulso del 2º compás, si bien después veremos casos en los que se sigue el procedimiento contrario. Aquí tenéis dos ejemplos de equivalencias del tipo "pulso igual a pulso". La velocidad con la que marcaríamos los pulsos sería siempre la misma. Podríamos poner el metrónomo al principio del fragmento y dejarlo sonar todo el tiempo. Sin embargo, al llegar al 9/8 tendríamos que hacer las corcheas más rápidas que las 2 corcheas del 3/4, para que entren 3 en un pulso. Serían tan rápidas como las del tresillo del 3/4.


Hay algunos autores que escriben la equivalencia con las figuras al revés. Puede resultar algo lioso (de hecho, lo encontraréis en muy pocos libros), pero conviene que conozcáis también esta forma de escribir las equivalencias, por si algún día las encontráis. Estos autores escriben en primer lugar la figura del pulso nuevo y la igualan con el pulso del compás precedente. Por eso escriben al final la abreviatura prec. Con ese sistema (que es minoritario), el fragmento anterior se escribiría así. El pulso del 9/8 (negra con puntillo) duraría lo mismo que el pulso del compás precedente (negra).

Caso 2: Hasta ahora hemos visto que si cambiaba el tipo de subdivisión del compás (de subdivisión binaria a ternaria o viceversa) y manteníamos el pulso, la velocidad de las figuras cambiaba (las corcheas del 9/8 no eran iguales a las corcheas del 3/4 sino a las corcheas especiales del tresillo). 
Puede darse el caso contrario: que las figuras permanezcan siempre iguales y que lo que cambie sea la velocidad del pulso. Para eso se utilizan las equivalencias de figura igual a figura, que suelen expresarse con "corchea = corchea".
En el siguiente ejemplo, las corcheas de todo el ejercicio serían iguales (y por tanto, el resto de figuras también serían iguales entre sí). Si en el pulso de 3/4 entran 2 corcheas y en el de 9/8 entran 3, el pulso del 9/8 será más amplio y por tanto se marcará más despacio. Si más adelante volvemos a un compás en el que el pulso sea de negra, el pulso volverá a marcarse más rápido.
¿Crees que en este caso podríamos solfear todo el ejercicio con el metrónomo puesto? La respuesta es que no, a menos que subdividiésemos los compases y pusiésemos el metrónomo a marcar corcheas. Desde luego no podemos hacerlo con el metrónomo marcando los pulsos, pues en cada cambio de compás, tendríamos que variar la velocidad del metrónomo.

MUY IMPORTANTE: las equivalencias de figura = figura son las más habituales. Eso significa que si en la partitura no viene indicada ninguna equivalencia, debemos seguir la de corchea = corchea. La velocidad del pulso no cambiaría si hacemos pasos entre compases con el mismo denominador, pero la velocidad cambiaría si hacemos pasos entre compases con denominadores distintos (y por tanto con figuras distintas para cada pulso). Por supuesto, podemos encontrar alguna rara excepción (por ejemplo, si en una pieza todas las equivalencias son de pulso = pulso y de repente el autor no escribe alguna, pero se sobreentiende que todas son iguales).

Caso 3: La velocidad del 2º compás no guarda relación con la del primer compás: no se mantienen las figuras ni el pulso. En estos casos no hay equivalencia, sino que encontramos una indicación de tempo nueva o una indicación metronómica nueva, que no guarde relación matemática con las anteriores. Por ejemplo: pasar de andante a allegro o de negra = 60 a negra = 76 o tener una indicación del tipo "più animato" (que significa, más animado). Estos cambios suelen hacerse de manera aproximada, yendo un poco más rápido o un poco más lento según las indicaciones. Generalmente, suele haber un calderón o una pequeña parada antes del cambio, para dar tiempo al intérprete a pensar el nuevo tempo.

Casos especiales: En raras ocasiones, el tempo en los cambios de compás no viene especificado con equivalencias, sino con indicaciones metronómicas. En esos casos hay que calcular si las indicaciones metronómicas guardan una relación matemática que permita traducirlas en "figura igual a figura" o en "pulso igual a pulso".
Si a una figura le corresponde una indicación metronómica X, a la figura inmediatamente inferior le corresponderá el doble de velocidad y a la figura inmediatamente superior le corresponderá la mitad de velocidad. Por ejemplo: si la negra es igual a 80, la corchea iría a 160 y la blanca iría a 40.
En el siguiente ejemplo... ¿crees que el cambio de compás se haría con pulso=pulso, con figura=figura o con cambio total de velocidad como en el caso 3 de las explicaciones?

La respuesta sería: pulso=pulso. ¿Por qué? La corchea del 3/4 va a 120, por lo que la negra (que equivale a un pulso) iría a 60. La corchea del 9/8 va a 180: dividiendo entre 3 me daría que la negra con puntillo (que equivale a un pulso en este compás) iría también a 60.

Actualización: aquí tenéis un ejercicio para que comprobéis si habéis entendido el proceso.
Ejercicio de equivalencias

Cambios de compás: las equivalencias

Publicado el por
Es frecuente encontrar obras en las que se producen cambios de compás. En determinado momento de la partitura, podemos encontrar una doble barra y una indicación de compás diferente a la inicial. No por ello se detiene la pieza, sino que la música debe pasar fluidamente de un compás a otro.
Puede haber varias posibilidades:
1. Que la velocidad del pulso se mantenga (lo que se indica con las llamadas equivalencias de pulso igual a pulso)
2. Que la velocidad del pulso cambie, pero la duración de las figuras se mantenga (lo que se indica con las llamadas equivalencias de figura igual a figura)
3. Que la velocidad del pulso y de las figuras cambie (lo que se indica con nuevas expresiones de tempo)

¿Cómo sabemos si la velocidad del pulso debe cambiar o no? Gracias a las equivalencias. Las equivalencias son relaciones entre dos figuras, cada una perteneciente a un compás distinto, que van a tener la misma duración y por eso van unidas por el símbolo =.

Caso 1: Si queremos que la velocidad del pulso se mantenga, escogemos las figuras que ocupan un pulso en cada compás y las igualamos. Para pasar de 2/4 a 3/4, escribiría "negra = negra" y para pasar de 2/4 a 6/8 escribiría "negra = negra con puntillo", ya que la figura que ocupa un pulso en 6/8 es la negra con puntillo.
La equivalencia se escribiría sobre la doble barra. Por lo general, la primera figura equivale al pulso del primer compás y la segunda figura equivale al pulso del 2º compás, si bien después veremos casos en los que se sigue el procedimiento contrario. Aquí tenéis dos ejemplos de equivalencias del tipo "pulso igual a pulso". La velocidad con la que marcaríamos los pulsos sería siempre la misma. Podríamos poner el metrónomo al principio del fragmento y dejarlo sonar todo el tiempo. Sin embargo, al llegar al 9/8 tendríamos que hacer las corcheas más rápidas que las 2 corcheas del 3/4, para que entren 3 en un pulso. Serían tan rápidas como las del tresillo del 3/4.


Hay algunos autores que escriben la equivalencia con las figuras al revés. Puede resultar algo lioso (de hecho, lo encontraréis en muy pocos libros), pero conviene que conozcáis también esta forma de escribir las equivalencias, por si algún día las encontráis. Estos autores escriben en primer lugar la figura del pulso nuevo y la igualan con el pulso del compás precedente. Por eso escriben al final la abreviatura prec. Con ese sistema (que es minoritario), el fragmento anterior se escribiría así. El pulso del 9/8 (negra con puntillo) duraría lo mismo que el pulso del compás precedente (negra).

Caso 2: Hasta ahora hemos visto que si cambiaba el tipo de subdivisión del compás (de subdivisión binaria a ternaria o viceversa) y manteníamos el pulso, la velocidad de las figuras cambiaba (las corcheas del 9/8 no eran iguales a las corcheas del 3/4 sino a las corcheas especiales del tresillo). 
Puede darse el caso contrario: que las figuras permanezcan siempre iguales y que lo que cambie sea la velocidad del pulso. Para eso se utilizan las equivalencias de figura igual a figura, que suelen expresarse con "corchea = corchea".
En el siguiente ejemplo, las corcheas de todo el ejercicio serían iguales (y por tanto, el resto de figuras también serían iguales entre sí). Si en el pulso de 3/4 entran 2 corcheas y en el de 9/8 entran 3, el pulso del 9/8 será más amplio y por tanto se marcará más despacio. Si más adelante volvemos a un compás en el que el pulso sea de negra, el pulso volverá a marcarse más rápido.
¿Crees que en este caso podríamos solfear todo el ejercicio con el metrónomo puesto? La respuesta es que no, a menos que subdividiésemos los compases y pusiésemos el metrónomo a marcar corcheas. Desde luego no podemos hacerlo con el metrónomo marcando los pulsos, pues en cada cambio de compás, tendríamos que variar la velocidad del metrónomo.

MUY IMPORTANTE: las equivalencias de figura = figura son las más habituales. Eso significa que si en la partitura no viene indicada ninguna equivalencia, debemos seguir la de corchea = corchea. La velocidad del pulso no cambiaría si hacemos pasos entre compases con el mismo denominador, pero la velocidad cambiaría si hacemos pasos entre compases con denominadores distintos (y por tanto con figuras distintas para cada pulso). Por supuesto, podemos encontrar alguna rara excepción (por ejemplo, si en una pieza todas las equivalencias son de pulso = pulso y de repente el autor no escribe alguna, pero se sobreentiende que todas son iguales).

Caso 3: La velocidad del 2º compás no guarda relación con la del primer compás: no se mantienen las figuras ni el pulso. En estos casos no hay equivalencia, sino que encontramos una indicación de tempo nueva o una indicación metronómica nueva, que no guarde relación matemática con las anteriores. Por ejemplo: pasar de andante a allegro o de negra = 60 a negra = 76 o tener una indicación del tipo "più animato" (que significa, más animado). Estos cambios suelen hacerse de manera aproximada, yendo un poco más rápido o un poco más lento según las indicaciones. Generalmente, suele haber un calderón o una pequeña parada antes del cambio, para dar tiempo al intérprete a pensar el nuevo tempo.

Casos especiales: En raras ocasiones, el tempo en los cambios de compás no viene especificado con equivalencias, sino con indicaciones metronómicas. En esos casos hay que calcular si las indicaciones metronómicas guardan una relación matemática que permita traducirlas en "figura igual a figura" o en "pulso igual a pulso".
Si a una figura le corresponde una indicación metronómica X, a la figura inmediatamente inferior le corresponderá el doble de velocidad y a la figura inmediatamente superior le corresponderá la mitad de velocidad. Por ejemplo: si la negra es igual a 80, la corchea iría a 160 y la blanca iría a 40.
En el siguiente ejemplo... ¿crees que el cambio de compás se haría con pulso=pulso, con figura=figura o con cambio total de velocidad como en el caso 3 de las explicaciones?

La respuesta sería: pulso=pulso. ¿Por qué? La corchea del 3/4 va a 120, por lo que la negra (que equivale a un pulso) iría a 60. La corchea del 9/8 va a 180: dividiendo entre 3 me daría que la negra con puntillo (que equivale a un pulso en este compás) iría también a 60.

Actualización: aquí tenéis un ejercicio para que comprobéis si habéis entendido el proceso.
Ejercicio de equivalencias